Understanding The Inner Workings Of Bloom Filters
If you’re like me, you’ve wondered how sites like Facebook, Reddit, and Instagram are able to tell you whether a username has been taken so quickly. It seemed like these services were able to search through hundreds of millions of user records to verify the uniqueness of a prospective username in no time at all.
After some research, I came across the data structure that is responsible for this speed – a probabilistic data structure called the bloom filter.
Overview
Bloom filters share some similarities with traditional sets. Generally speaking, a set will tell you with certainty whether it contains a particular element or not. Bloom filters, however, make a slightly different promise.
They are probabilistic data structures which means they’ll tell you with certainty whether an element is not in the set and they’ll tell you if it is probably in the set. In other words, there’s a chance that bloom filters will return a false positive. That is, they’ll incorrectly claim that the set contains an element that was never added.
Maybe you’re wondering why a data structure that can only probably tell you if it contains an element is useful? Well, bloom filters are extremely fast and memory-efficient as we’ll soon see. Sometimes the speed and scalability of a solution are more important than the occasional false positives. In practice, if you know what your acceptable false positive rate is, you can calculate an initial size for the bloom filter to guarantee that rate.
Implementation
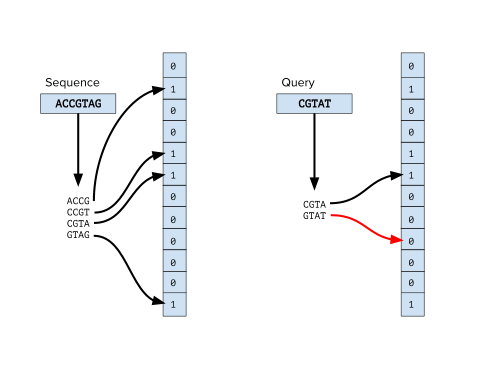
Bloom filters are simply a bit array of m bits all initially set to 0. We’ll also need k different hash functions. These functions will be run over whatever item we are trying to add to the set and will return the indices in the bloom filter to turn from a 0 to a 1.
It’s important that whatever hash functions we choose create a uniform random distribution for best results. There are many industry standard options to pick from: HashMix, murmur, and the fnv series – just to name a few.
Generally, the number of hash functions needed would be a small constant derived from whatever false positive rate is acceptable for your use case.
Initialization
Let’s take an empty bloom filter and add an element to it.
let size = 10
let bloomFilter = Array(repeating: false, count: size)
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Adding an element
To add an element, we’ll take the element we want to add and pass it to all k hash functions to get k array indices. We’ll set the value at those indices to 1.
In practice, these would not be 3 distinct hashing algorithms. Instead, it’d likely be the same algorithm just seeded with a different value (i.e. 1 … k) which will generate k distinct hash functions.
bloomFilter[hashAlgorithm1(“digital”) % size] = true
bloomFilter[hashAlgorithm2(“digital”) % size] = true
bloomFilter[hashAlgorithm3(“digital”) % size] = true
Now, it might look something like this:
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
And after adding a few more entries to the set:
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
Querying
If we wanted to query for an element, we’d do the same operations to get the k array indices. Then, if any of the bits at those indices are 0, we know definitively that the value is not in the set. Instead, if all of the indices values are 1, we know that the value is probably in the set – remember it could still be a false positive.
bloomFilter.search(“digital”) which in turn calls:
bloomFilter[hashAlgorithm1(“digital”) % size] // 2
bloomFilter[hashAlgorithm2(“digital”) % size] // 6
bloomFilter[hashAlgorithm3(“digital”) % size] // 7
So, to check if the element is in the set, we just need to check indices 2,6, and 7 and verify they are set to 1.
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
So, now we know that “digital” is probably in the set.
Limitations
It’s important to understand that elements can only be added to bloom filters and never removed. We can’t reset particular bits back to 0 because we don’t know if there’s some other element in the set that also maps to those indices. For example, after passing through the hash functions, “dog” and “cat” might share the exact same indices.
Remember the filter isn’t storing the data anywhere unlike traditional sets, arrays, etc, it’s just turning on certain indices. So, there’s no way of checking what word a particular set of indices relates to.
Big O
Implementing bloom filters requires us to specify the size upfront, so we can’t enlarge the data structure later. As a result, the more elements we add to the filter, the higher the error rate rises. So, it’s important to choose an initial size for the bloom filter that can scale with your data and allows you to keep a maintainable error rate.
add(): O(k)
contains(): O(k)
where k is the number of hash functions.
One of the key advantages of bloom filters is that the time to add or check for inclusion in the set is constant; it’s completely independent of the number of items in the set.
Wrapping up
Bloom filters are used everywhere. Chances are in just getting to this site you’ve encountered one. Chrome uses a local Bloom filter to store malicious URLs. Before navigating to a site, the browser will check if the site exists in the set of malicious URLs and if it does it’ll perform a full check on Google’s servers.
Hope you enjoyed this post! Check out some of my other posts below!
